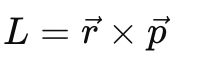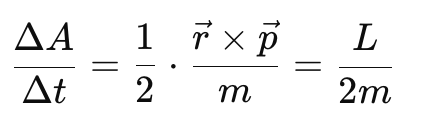Gravitation

Gravitation is one of the fundamental forces of nature studied in Physics. It is the attractive force that pulls objects toward each other, keeping planets in orbit and giving weight to everything on Earth. This universal force governs the motion of celestial bodies as well as everyday phenomena around us.

Previous year Questions

Year	Question	Marks
2023	Write Kepler’s second law of planetary motion. On which conservation principle it isbased ?	2M
2016 Special exam	Write Kepler’s law of planetary motion.	5M

What is Gravitation?

• Gravitation is a force of attraction that exists between any two objects with mass.
• It is one of the four fundamental forces of nature, along with electromagnetism, weak nuclear force, and strong nuclear force.
• Unlike other forces, gravitational force is always attractive.

Historical Perspective

• Aristotle believed that heavier objects fall faster than lighter objects.
• Galileo Galilei disproved Aristotle by demonstrating that objects fall at the same rate in the absence of air resistance.
• Kepler: Laws of planetary motion that laid the foundation for understanding orbital mechanics.
• Sir Isaac Newton formulated the Law of Universal Gravitation in the 17th century, which accurately described the force of attraction between two masses.
• Einstein: General relativity, describing gravity as the curvature of space-time, rather than a force.
• Modern Physics: Ongoing research into quantum gravity, black holes, and gravitational waves.

The Study of Celestial Bodies:

• Early observations of stars and planets:
  • Stars remain fixed in their positions year after year.
  • Planets move against the background of stars, exhibiting regular motions.
• The Geocentric model (Ptolemy, 2000 years ago):
  • Earth was at the center, and all celestial bodies revolved around it in circular orbits.
• The Heliocentric model (Aryabhata, 5th century A.D.):
  • Proposed the Sun as the center of the solar system, with planets revolving around it.
• Nicolas Copernicus (1473-1543) revived the heliocentric model, despite facing opposition from the Church.
  • Galileo supported Copernicus’ theory and faced prosecution for his beliefs.

Tycho Brahe and Johannes Kepler:

• Tycho Brahe (1546-1601) recorded extensive observations of planets with the naked eye.
• Johannes Kepler (1571-1640) analyzed Brahe’s data and formulated three laws of planetary motion.
  • These laws, known as Kepler’s Laws, played a key role in the development of Newton’s universal law of gravitation.

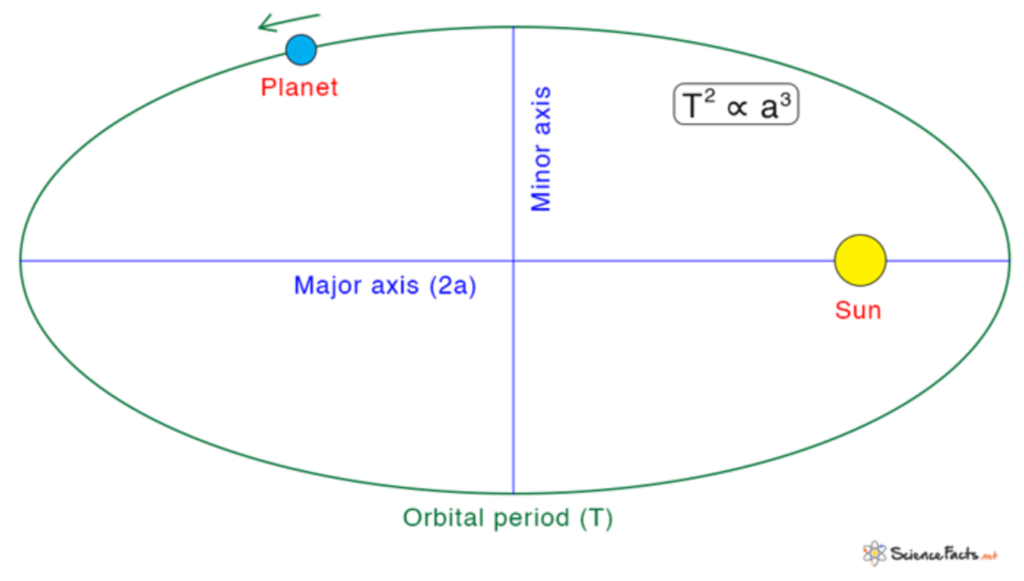
KEPLER’S LAWS OF PLANETARY MOTION

Law of Orbits:

• All planets move in elliptical orbits with the Sun at one of the foci of the ellipse.
  • This law deviates from the Copernican model, which assumed circular.

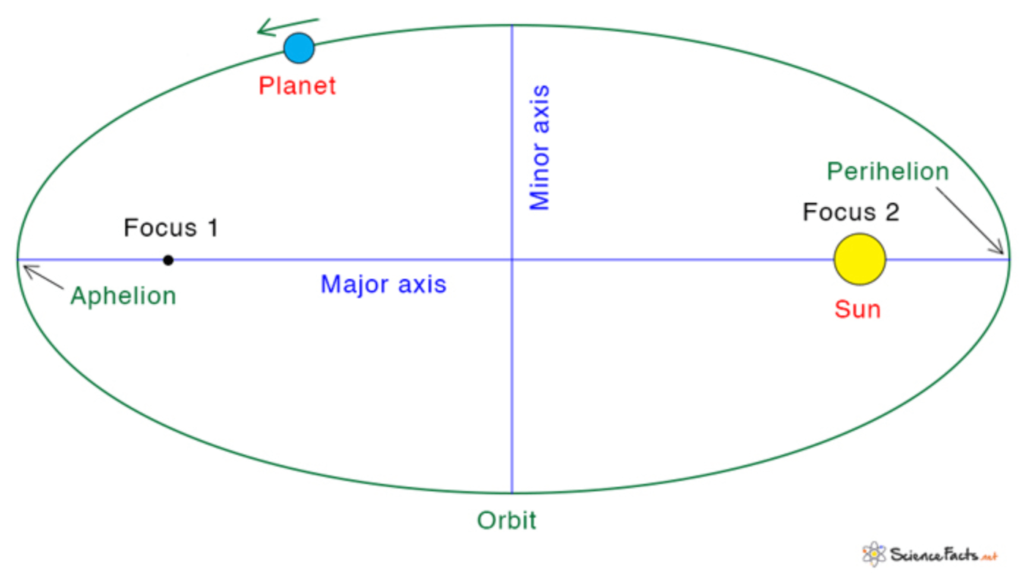
Law of Areas:

• The line joining any planet to the Sun sweeps out equal areas in equal intervals of time.
  • This explains the change in speed of planets when they are nearer or farther from the Sun.

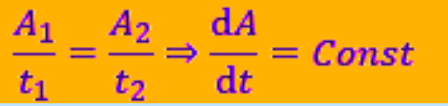
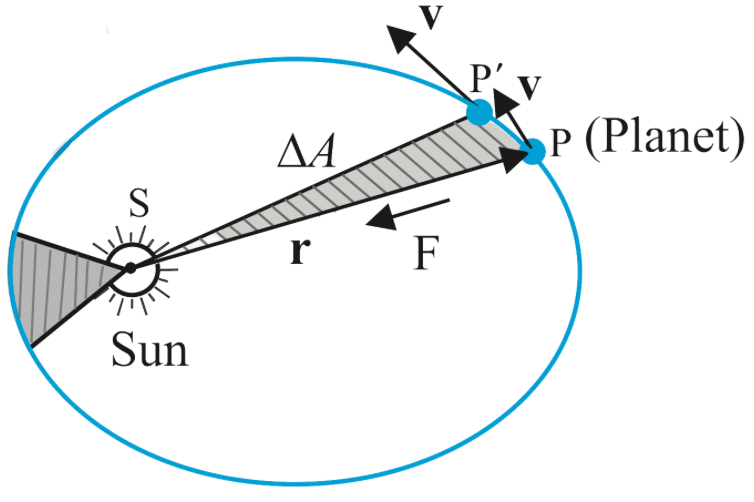
EXPLANATION

The law of areas can be understood through conservation of angular momentum (valid for central forces like gravity):

Angular Momentum (L): Given by 

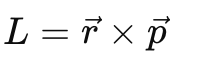
The area swept by the planet in time interval ∆t is given by:

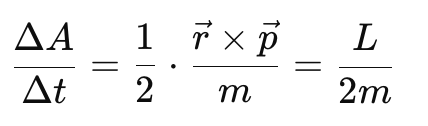
• where m is the planet’s mass and L is constant for a central force.
  • Thus, the rate of area swept out by the planet remains constant, demonstrating the Law of Areas.
  • Since gravitation is a central force, the law of areas follows naturally.

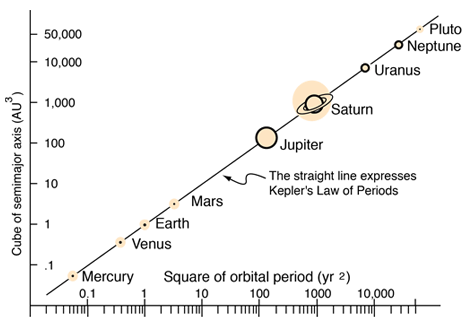
Law of Periods:

• The square of the time period of a planet’s revolution around the Sun is proportional to the cube of the semi-major axis of its elliptical orbit.

T²∝a³

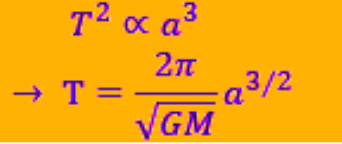
• Where:
  • T is the orbital period,
  • a is the semi-major axis of the ellipse.

These laws formed the foundation for Newton’s law of gravitation and remain essential for understanding planetary motion.

UNIVERSAL LAW OF GRAVITATION

• Newton was inspired by observing an apple fall from a tree to formulate the Universal Law of Gravitation.
• His reasoning was based on the motion of the Moon around Earth, which led to an explanation of terrestrial gravitation and Kepler’s laws.

Newton’s law of gravitation states that every particle in the universe attracts every other particle with a force that is:

• Directly proportional to the product of their masses.
• Inversely proportional to the square of the distance between them.
• Directed along the line joining the two masses.

Mathematical Formulation:

The force F on a point mass m2 due to another point mass m1 has the magnitude

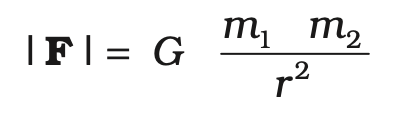
Vector Form of the Law

• Let:
  • r₁​ and r₂​ are the position vectors of two masses m₁​ and m₂.
  • r₁₂=r₂−r₁ be the displacement vector from m₁ to m_2.
  • r̂ be the unit vector in the direction of r.
  • r=∣r∣ be the magnitude of the separation.
  • Then, the gravitational force exerted on m₁​ by m₂​ is:

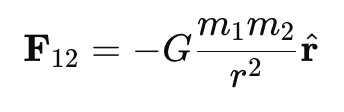
Similarly, the force exerted on m₂ ​ by m(using Newton’s Third Law) is:

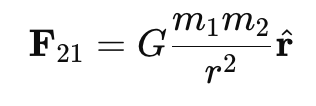
where:

• G is the gravitational constant (6.674×10^-11 N⋅m²/kg² ).
• r̂ = r/r​ is the unit vector along the line joining the two masses.
• The negative sign in F₁₂​ indicates that gravity is always an attractive force.

THE GRAVITATIONAL CONSTANT (G)

• The value of G was first measured by Henry Cavendish in 1798 using the torsion balance experiment.

Cavendish’s Experiment

• He used a horizontal bar suspended by a fine wire.
• Two small lead spheres were attached to the ends of the bar.
• Two larger lead spheres were placed nearby.
• The gravitational attraction between the small and large spheres caused the bar to rotate.
• By measuring the angle of rotation and the restoring force of the wire, he calculated G.

Final Value of G(Refined Measurements):

• G = 6.674×10^-11 N⋅m²/kg²

Significance of G

• Universal Constant → Same everywhere in the universe.
• Determines Gravitational Force → Crucial for understanding planetary motion, orbits, and cosmic structures.
• Used in Einstein’s General Relativity → Appears in the equation for spacetime curvature.

Significance of  Gravitational force

• Gravity on Earth imparts weight to physical objects
• Tidal Forces: Gravitational forces between celestial bodies, such as the Earth and the Moon, lead to tidal effects. Tidal forces influence ocean tides on Earth, affecting coastal regions.
• The original gaseous matter in the universe came together due to gravitational attraction, leading to the formation of stars that later condensed into galaxies. Therefore, gravity plays a crucial role in shaping many large-scale structures in the universe.
• Gravitational force is responsible for the orbits of celestial bodies.  It keeps planets in orbit around the Sun, moons around planets, and stars within galaxies.
• the motion of the moon around the earth

Free Fall

• Free fall refers to the motion of an object when it is falling under the sole influence of gravity, without any other forces acting on it.  In a vacuum or in the absence of significant air resistance, all objects near the surface of the Earth, regardless of their mass, will experience the same acceleration due to gravity.
• This rate is called the acceleration of gravity, on Earth this rate is 9.81 m/sec². We use the symbol g to represent this value. {This means you add almost 10 m/s to your speed every second you spend falling. After 3 seconds falling, you are moving over 29 m/s, that’s almost 66 mph!}
• (Acceleration means that the velocity at which an object moves is changing in a steady way.)

This principle is famously demonstrated by the story of Galileo dropping different objects from the Leaning Tower of Pisa, where he found that they all hit the ground simultaneously.

ACCELERATION DUE TO GRAVITY OF THE EARTH

Gravitational Force  on the body

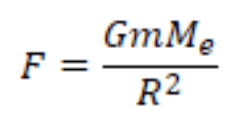
(ignoring height in  comparison to  radius of earth)

according  to Newton’s 2nd  Law

F = mg

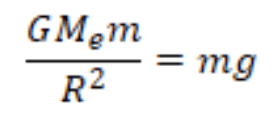
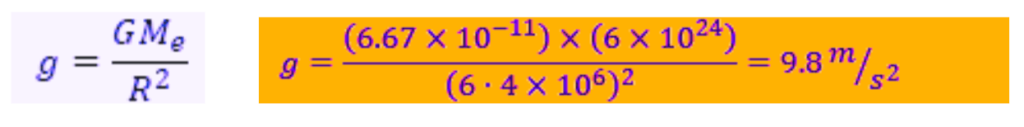
ACCELERATION DUE TO GRAVITY BELOW AND ABOVE THE SURFACE OF EARTH

Gravitational Acceleration is the acceleration ,i.e. rate of Change in velocity in free fall

• results in steady gain in speed
• at different points, ranges from 9.764 m/s² to 9.834 m/s² depending on altitude, latitude and longitude.
• Standard Value – 9.80665 m/s² (ignoring drag)

Above the Surface

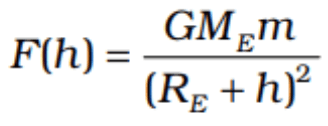
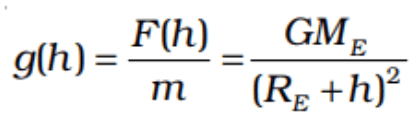
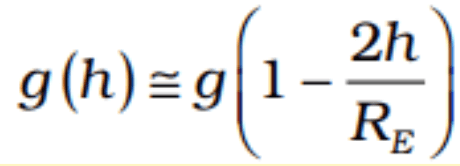
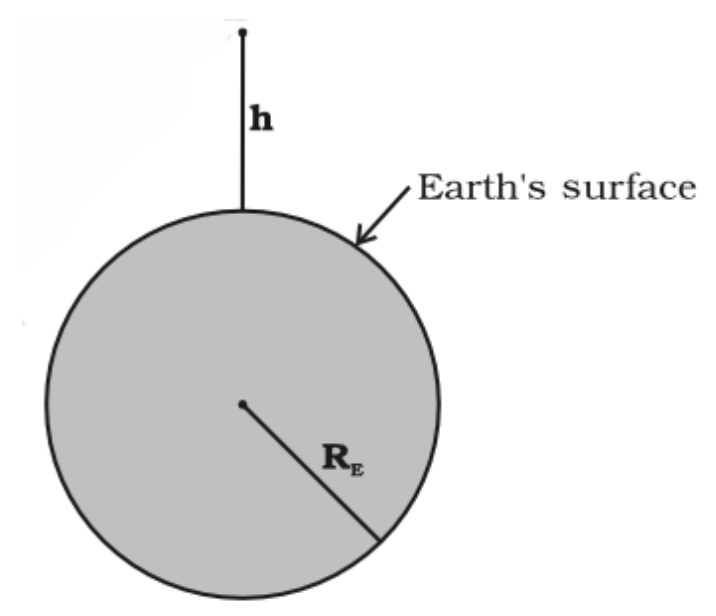
for small heights h above the value of g decreases by a factor (1−2h/R_e ).

Below the Surface

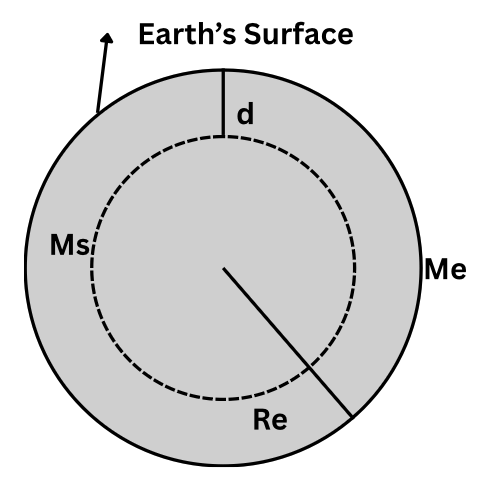
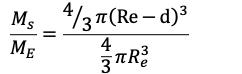
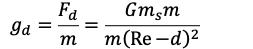
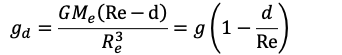
Due to earth’s rotation

• increases as we move from equator to the Poles

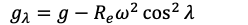
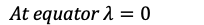
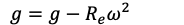
Equator:

• At the equator, the Earth’s rotation imparts an outward centrifugal force due to its rotation -> effectively reducing the net acceleration due to gravity.
• “g” is slightly smaller compared to what it would be if the Earth were not rotating.

Poles:

• At the poles, there is minimal effect from the Earth’s rotation, and the acceleration due to gravity is closer to its theoretical maximum.

Thus, The equatorial bulge caused by the Earth’s rotation also contributes to the differences in “g” between the equator and the poles.

Gravity at Moon

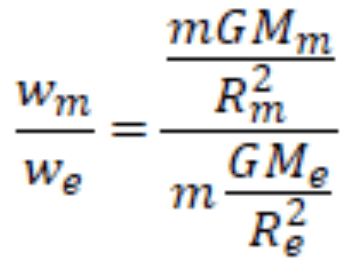
• An object on the Moon weighs only 1/6th of what it does on Earth.
• But its mass stays exactly the same.

Gravitational Field

Describes the influence of a massive object on the space around it.  At any point in space, the gravitational field represents the force per unit mass that a test mass would experience if placed at that location.

Direction:

• The gravitational field points towards the massive object creating it. For example, near the Earth’s surface, the gravitational field points towards the center of the Earth.
• Strength of the gravitational field is stronger closer to the massive object and decreases with distance following an inverse-square law.

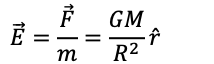
Gravitational Potential Energy

• Gravitational potential energy is energy an object possesses because of its position in a gravitational field.
• Gravitational potential energy is equal to the work done against gravity to bring a mass to a given point in space.
• Because of the inverse square nature of the gravity force, the force approaches zero for large distances, and it makes sense to choose the zero of gravitational potential energy at an infinite distance away.

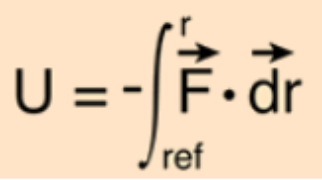
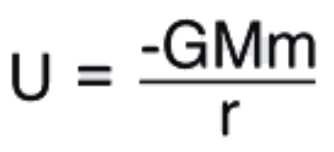
Gravitational Potential

• Gravitational potential is a scalar field that describes the gravitational potential energy per unit mass at any point in space surrounding a massive object.
• It represents the work that would be done by gravity in moving a unit mass from a reference point to a specific location in the gravitational field.
• The gravitational force is a conservative force, and therefore a potential energy function can be defined.

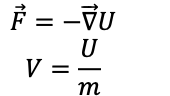
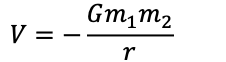
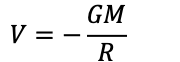
Escape Velocity

• Escape velocity is the minimum velocity an object must attain to break free from the gravitational attraction of a massive body.
• It is the speed at which the kinetic energy of an object equals the gravitational potential energy, allowing the object to overcome the gravitational pull and move away indefinitely.

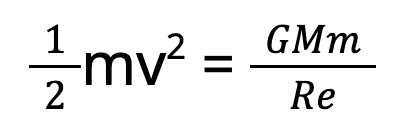
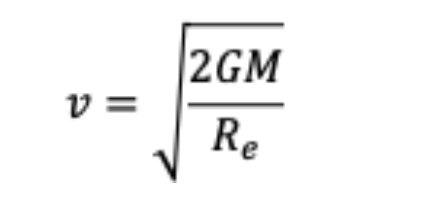
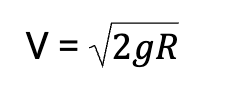
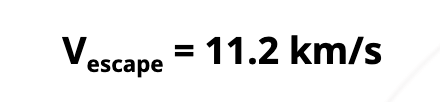
The escape speed for the moon turns out to be 2.3 km/s, about five times smaller. This is the reason that moon has no atmosphere. Gas molecules if formed on the surface of the moon having velocities larger than this will escape the gravitational pull of the moon.

Earth Satellite

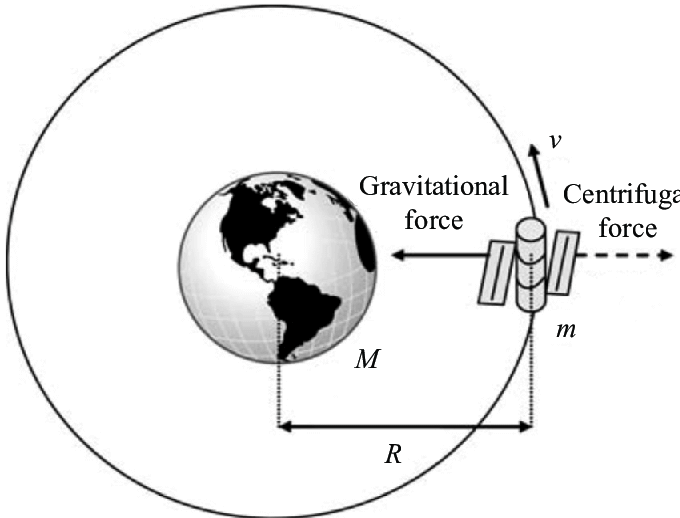
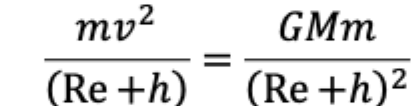
Velocity

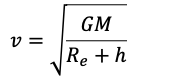
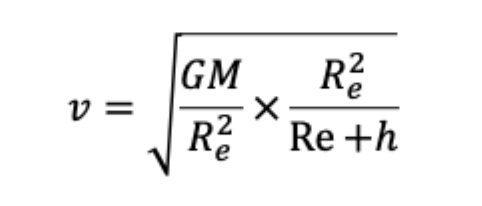
For satellite close to earth 

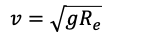
Time Period of Satellite:

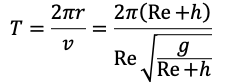
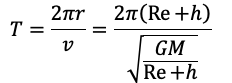
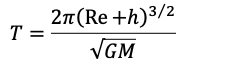
For Geostationary satellite:

T = 24 Hr  → H = 35800 km

Satellites in a circular orbits around the earth in the equatorial plane with T = 24 hours are called Geostationery Satellites. Clearly, since the earth rotates with the same period, the satellite would appear fixed from any point on earth.

For satellite close to earth:

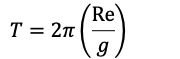
Which is approximately 85 minutes

Energy of Satellite:

The total energy of a circularly orbiting satellite is thus negative, with the potential energy being negative but twice the magnitude of the positive kinetic energy.

For Geostationary satellite:

• Geostationary satellites are positioned in circular orbits around the Earth’s equator with a period of approximately 24 hours, matching the Earth’s rotational period.
• Positioned at a distance of around 22,300 miles (35,800 kilometers) directly above the equator, these satellites rotate in the same direction as the Earth—from west to east.
• This synchronization with the Earth’s rotation allows geostationary satellites to maintain a constant position in the sky as observed from the ground. Essentially, they appear motionless, making them ideal for applications such as telecommunications, weather monitoring, and Earth observation, as they provide continuous coverage over a specific region without the need for constant adjustment or tracking.

Mass vs Weight

Mass (m)	Weight (W)
Mass is a measure of the amount of matter in an object. It is an intrinsic property and does not depend on the object’s location. • only Magnitude	Weight is the force exerted on an object due to gravity. • It depends on both the mass of the object and the acceleration due to gravity• It has both magnitude and direction
The standard unit of mass is the kilogram (kg).	The standard unit of weight is the newton (N) in the SI system.
Mass is directly related to an object’s inertia, which is its resistance to changes in motion.	W = mgFor example, an object will weigh less on the Moon than on Earth due to the Moon’s weaker gravitational field, but its mass remains the same.

Weightlessness

• Weightlessness, often referred to as “zero gravity”, is the absence of weight sensation experienced by objects and individuals in free fall.
• Despite the term “zero gravity,” gravity is still present; however, the reaction force is absent  (R) = 0 . Basically, the notion of weight is because of the reaction force being applied on the object.
• If the cable of a lift coming in downward direction beaks, there will be free fall of the lift and we will experience weightlessness, i.e. zero weight.

Why Astronauts Appear to Float in a Satellite

1. Free Fall and Weightlessness:

Artificial satellites orbiting the Earth are actually in a continuous state of free fall towards the Earth. However, because they have a high tangential velocity, they keep missing the Earth—this creates an orbit.

• Everything inside the satellite, including astronauts and objects, is falling with the same acceleration due to gravity.
• Since there is no contact force acting on the body (i.e., the normal reaction R=0), astronauts experience apparent weightlessness.

2. Gravitational vs. Centrifugal Force:

In orbit:

• The gravitational force pulling the satellite towards the Earth is balanced by the centrifugal force due to its circular motion.
• This balance creates a microgravity environment, where the net force felt by objects inside the satellite is almost zero.

3. No Up or Down:

In space, without a ground to push against or a fixed vertical direction:

• There is no natural “up” or “down”.
• Orientation becomes relative, based on the position of objects or the satellite interior.

4. Curious Effects in Microgravity:

In this unique environment, everyday phenomena behave differently:

• Water in a glass: If an astronaut turns a glass upside down, the water won’t fall.
• Instead, water floats in the form of droplets because there’s no gravity to pull it down.
• As a result, astronauts cannot drink from an open glass. They use special straws or containers designed for zero-gravity environments.

FAQ (Previous year questions)